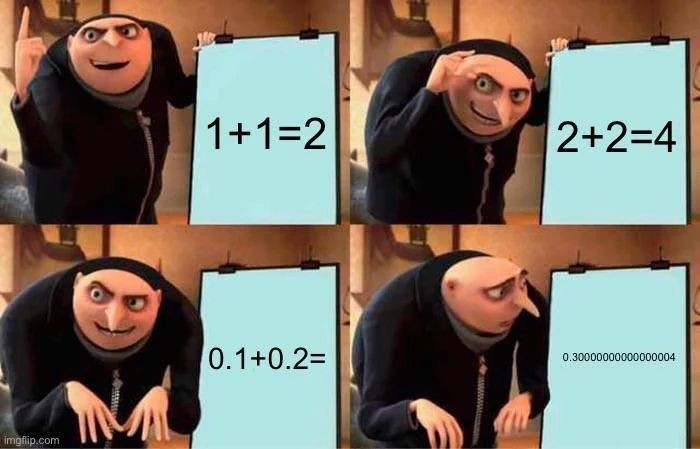• Turun@feddit.de
      12·
      2 years ago

      Are you sure? I’ve never seen that inequality before.

      Edit: and at least python agrees with me

      print(0.1 + 0.2)  # 0.300...0004
print(1.0-1.0)  # 0.0
      • h3ndrik@feddit.de
        3·
        2 years ago

        I think it’s equal zero in this case. I’d have to look up the IEEE specification to make sure. AFAIK it’s just not guaranteed for any numbers and depends on the floating point implementation. A general rule of thumb for programmers is not to use ‘equal’ with floating point numbers.

        • Turun@feddit.de
          9·
          2 years ago

          The example is wrong, because they used 1.0.

          But in general x-x does not have to equal 0, that is true. I’m pretty sure Nan and infinity would yield not 0.0, but Nan instead.

          And if you reach x with two different calculations, e.g. x1 = a - b - c and x2 = a - c - b it is certainly not guaranteed that x1 - x2 == 0.0